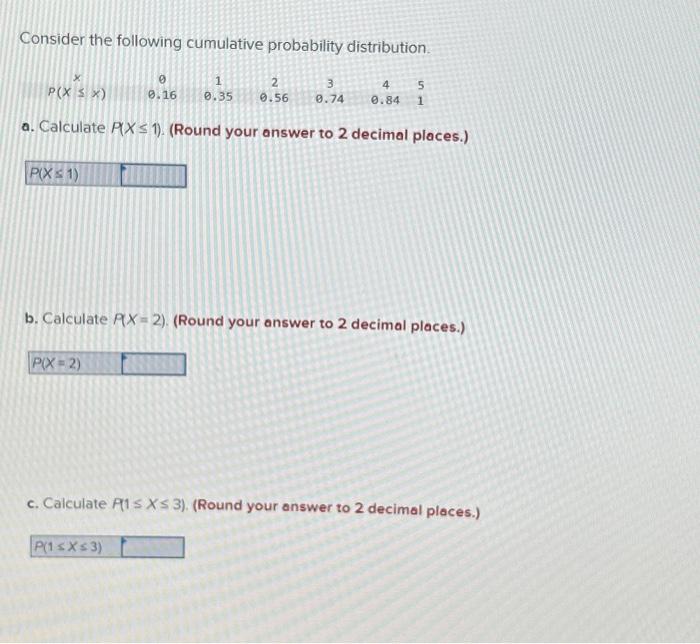
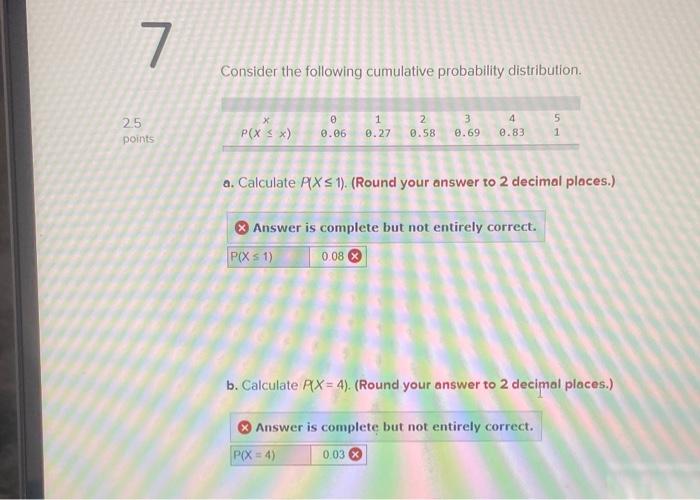
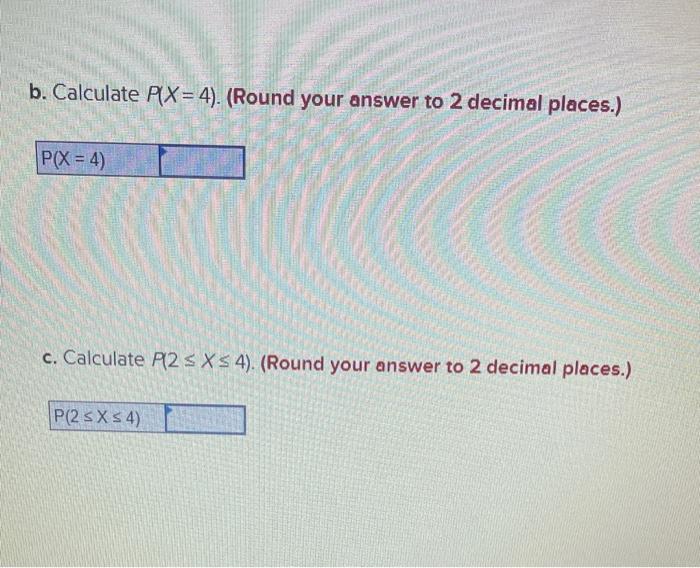
As we delve into the realm of probability, consider the following cumulative probability distribution, a cornerstone of statistical analysis. This mathematical tool provides a comprehensive understanding of the likelihood of events occurring within a given range, offering valuable insights across diverse fields.
Cumulative probability distribution, unlike probability density function, accumulates probabilities over a specified interval, providing a holistic view of the distribution’s behavior. Its properties, including monotonicity, boundedness, and continuity, form the foundation for its applications.
1. Define Cumulative Probability Distribution
A cumulative probability distribution (CDF) is a function that gives the probability that a random variable X takes on a value less than or equal to a given value x. It is defined as follows:
F(x) = P(X ≤ x)
where F(x) is the CDF of X.
The CDF is different from the probability density function (PDF) of X, which gives the probability that X takes on a specific value. The CDF is a non-decreasing function, while the PDF can be either increasing or decreasing.
2. Properties of Cumulative Probability Distribution
The CDF of a random variable X has several key properties:
- It is non-decreasing.
- It is bounded between 0 and 1.
- It is continuous if X is a continuous random variable.
3. Applications of Cumulative Probability Distribution
The CDF is used in a variety of applications, including:
- Statistics:The CDF is used to calculate probabilities, such as the probability that a sample mean falls within a certain range.
- Finance:The CDF is used to price options and other financial instruments.
- Engineering:The CDF is used to design systems that are reliable and safe.
4. Relationship between Cumulative Probability Distribution and Probability Density Function
The CDF and the PDF of a random variable X are related by the following equation:
F(x) = ∫ -∞xf(t) dt
where f(x) is the PDF of X.
This equation shows that the CDF can be obtained by integrating the PDF.
5. Visualizing Cumulative Probability Distribution
The CDF can be visualized using a cumulative distribution function (CDF) plot. A CDF plot is a graph of the CDF against x. The CDF plot can be used to see the distribution of X and to calculate probabilities.
6. Applications in Statistical Inference
The CDF is used in a variety of statistical inference procedures, such as hypothesis testing and confidence interval estimation. In hypothesis testing, the CDF is used to calculate p-values. In confidence interval estimation, the CDF is used to calculate confidence intervals.
7. Numerical Methods for Computing Cumulative Probability Distribution: Consider The Following Cumulative Probability Distribution
There are a variety of numerical methods for computing the CDF of a random variable X. These methods include:
- Numerical integration:Numerical integration is a method for approximating the integral in the definition of the CDF.
- Monte Carlo simulation:Monte Carlo simulation is a method for generating random samples from a distribution and using these samples to estimate the CDF.
8. Examples of Cumulative Probability Distributions
There are a number of common cumulative probability distributions, including:
- Normal distribution:The normal distribution is a continuous distribution that is used to model a wide variety of phenomena.
- Binomial distribution:The binomial distribution is a discrete distribution that is used to model the number of successes in a sequence of independent experiments.
- Exponential distribution:The exponential distribution is a continuous distribution that is used to model the time between events.
9. Software for Analyzing Cumulative Probability Distribution

There are a number of software tools and packages that can be used to analyze cumulative probability distributions. These tools include:
- R:R is a free and open-source statistical software package that can be used to analyze cumulative probability distributions.
- Python:Python is a free and open-source programming language that can be used to analyze cumulative probability distributions.
- MATLAB:MATLAB is a commercial software package that can be used to analyze cumulative probability distributions.
FAQ Compilation
What is the key difference between cumulative probability distribution and probability density function?
Cumulative probability distribution accumulates probabilities over an interval, while probability density function represents the probability of a specific value.
How is cumulative probability distribution used in hypothesis testing?
It helps determine p-values, which play a crucial role in assessing the significance of statistical results.