Delve into the captivating world of functions and their graphs with Unit 2 Functions and Their Graphs Homework 1, an exploration that unveils the intricacies of these mathematical concepts. From linear to exponential functions, prepare to navigate a landscape of equations and their corresponding visual representations, gaining insights into their behavior and real-world applications.
This comprehensive guide will provide a detailed breakdown of the homework assignment, offering strategies for problem-solving, identifying common pitfalls, and exploring the practical significance of functions in various fields. Get ready to unlock the secrets of functions and their graphs, empowering you to tackle mathematical challenges with confidence.
Functions and Their Graphs
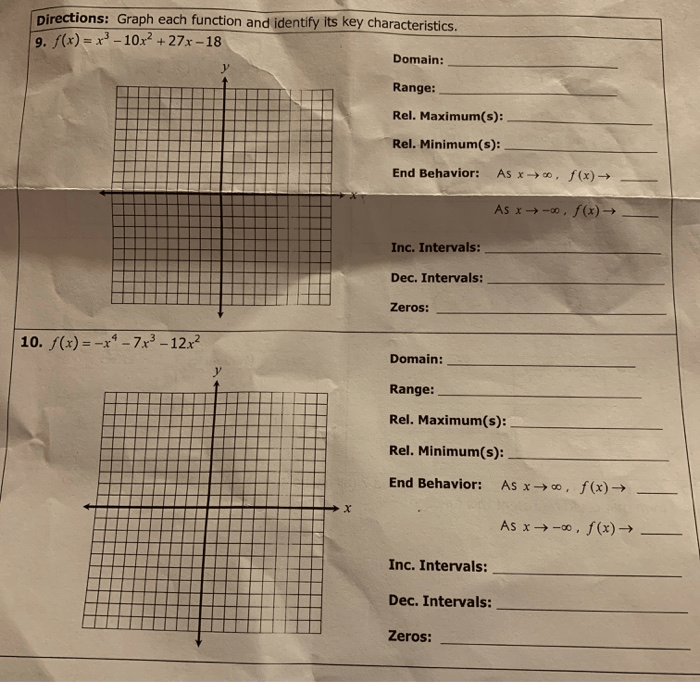
Functions are mathematical relationships that assign a unique output value to each input value within a specific domain. Their graphs provide visual representations of these relationships, allowing us to analyze and understand the behavior of functions.
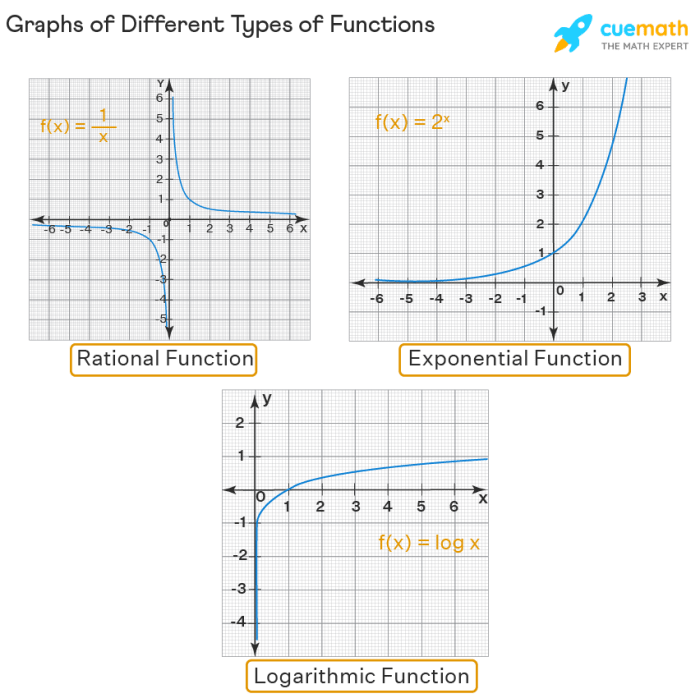
Different types of functions, such as linear, quadratic, and exponential, exhibit distinct graph shapes. Linear functions form straight lines, quadratic functions create parabolas, and exponential functions produce curves that increase or decrease rapidly.
To graph functions, we can use tables of values and plot the corresponding points. By connecting these points, we obtain the function’s graph, which provides insights into its characteristics, such as intercepts, extrema, and domain and range.
Homework 1: Unit 2 Functions and Their Graphs, Unit 2 functions and their graphs homework 1
This homework assignment focuses on various function-related problems, requiring students to analyze functions, graph them, and solve related questions.
| Problem Number | Description | Deliverables |
|---|---|---|
| 1 | Graph the linear function f(x) = 2x + 1 and determine its intercepts. | Graph and intercepts |
| 2 | Find the equation of the parabola that passes through the points (1, 2), (3, 8), and (-1, 0). | Equation of the parabola |
| 3 | Solve for x in the exponential equation 2x = 16. | Solution value(s) of x |
| 4 | Analyze the graph of the function f(x) = x3
|
Key points (intercepts, extrema) |
Strategies for Solving Problems
To effectively solve function-related problems, it is crucial to:
- Understand the function’s equation and its graph.
- Identify key points, such as intercepts and extrema, to analyze the function’s behavior.
- Use algebraic techniques and graphing tools to find solutions and make predictions.
Common Mistakes and Pitfalls
- Assuming that all functions are linear or quadratic.
- Ignoring the domain and range of functions when graphing.
- Making algebraic errors when solving for key points or finding solutions.
- Failing to consider the context of the problem and the units of measurement.
To avoid these pitfalls, it is essential to:
- Identify the type of function and its characteristics.
- Pay attention to the scale and units when graphing.
- Double-check algebraic calculations and solutions.
- Understand the real-world context and the implications of the function’s behavior.
Applications and Real-World Examples
Functions and their graphs find applications in various fields, including:
- Science:Modeling physical phenomena, such as projectile motion or radioactive decay.
- Engineering:Designing structures, analyzing circuits, and optimizing systems.
- Economics:Forecasting demand, analyzing market trends, and managing investments.
By understanding the concepts of functions and their graphs, we can solve problems, make predictions, and gain insights into the behavior of real-world systems.
Frequently Asked Questions: Unit 2 Functions And Their Graphs Homework 1
What is the main concept behind functions and their graphs?
Functions establish a relationship between two sets, where each element in the first set corresponds to exactly one element in the second set. Their graphs visually represent this relationship, providing insights into the function’s behavior and key features.
How can I effectively solve function-related problems?
Understanding the function’s equation and its graph is crucial. Analyze the equation to identify key points (intercepts, extrema) and study the graph to determine its shape, domain, and range. Employ algebraic and graphical techniques to solve problems efficiently.
What are some common mistakes to avoid when working with functions and their graphs?
Common pitfalls include misinterpreting the domain and range, incorrectly plotting points, and failing to consider the function’s behavior at key points. Pay close attention to the problem statement, use appropriate graphing techniques, and double-check your work to minimize errors.