Welcome to the intriguing world of box and whisker plot quiz, where you’ll embark on a journey to unravel data patterns and extract meaningful insights. Prepare to delve into a captivating exploration of this versatile graphical tool.
In this quiz, you’ll discover the components that make up a box and whisker plot, learn how to interpret its nuances, and master the art of creating one from a given dataset. Brace yourself for a thrilling adventure into the realm of data visualization and analysis!
Definition and Purpose
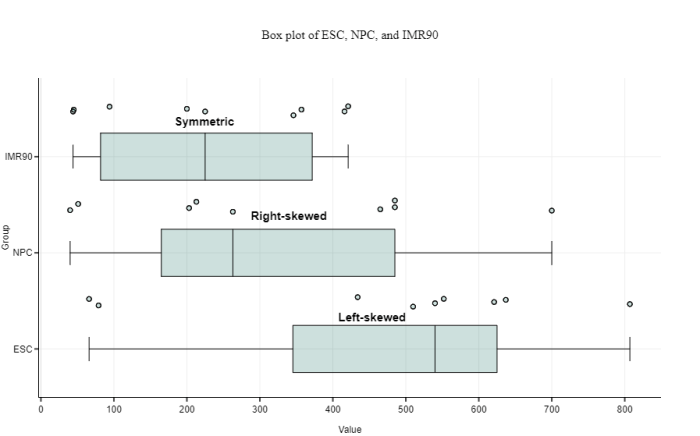
A box and whisker plot, also known as a boxplot, is a graphical representation of the distribution of data. It provides a visual summary of the data’s central tendency, variability, and spread.
The purpose of using a box and whisker plot is to quickly and easily identify the following characteristics of the data:
- Median: The middle value of the data when arranged in order from smallest to largest.
- Quartiles: The 25th and 75th percentiles, which divide the data into four equal parts.
- Interquartile range (IQR): The difference between the 75th and 25th percentiles, which represents the middle 50% of the data.
- Outliers: Data points that are significantly different from the rest of the data.
Components of a Box and Whisker Plot
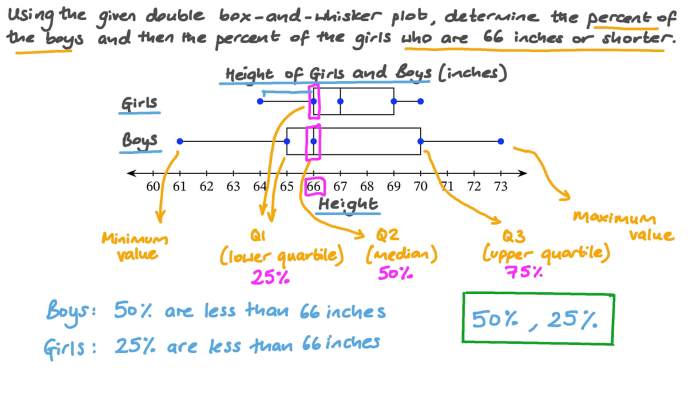
A box and whisker plot, also known as a boxplot, is a graphical representation of the distribution of data. It provides a quick and easy way to visualize the central tendency, spread, and skewness of the data.
Box and whisker plots are great for visualizing data. When you look at one, try to remember the cuando oyes algo usas el . This will help you understand the data better. Box and whisker plots are a great way to learn about data.
A box and whisker plot consists of several components, each of which represents a different aspect of the data distribution:
Minimum and Maximum
- The minimum value is the lowest value in the dataset.
- The maximum value is the highest value in the dataset.
Median
The median is the middle value in the dataset when the data is arranged in order from smallest to largest. It represents the point at which half of the data values are below and half are above.
Quartiles
- The first quartile (Q1) is the median of the lower half of the data.
- The third quartile (Q3) is the median of the upper half of the data.
Interquartile Range
The interquartile range (IQR) is the difference between the third quartile and the first quartile. It represents the spread of the middle 50% of the data.
Outliers
Outliers are data points that are significantly different from the rest of the data. They are typically represented by small circles or stars outside the box.
Each component of a box and whisker plot provides valuable information about the distribution of the data. By understanding the significance of each component, you can gain a deeper understanding of the data and make informed decisions.
Interpreting a Box and Whisker Plot: Box And Whisker Plot Quiz
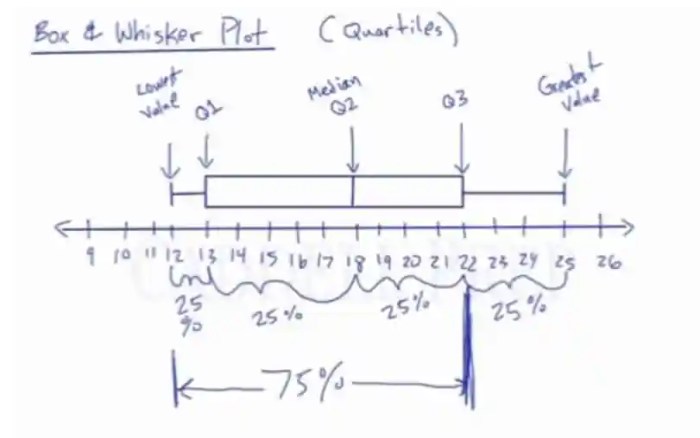
Interpreting a box and whisker plot provides valuable insights into the distribution and characteristics of a dataset. It helps identify central tendency, spread, skewness, and outliers, allowing for informed inferences about the underlying data.
Central Tendency
- The median, represented by a line within the box, divides the data into two equal halves.
- The mean, not directly shown on the plot, can be estimated by observing the position of the median within the box.
Spread
- The interquartile range (IQR), represented by the length of the box, measures the spread of the middle 50% of the data.
- The whiskers extend from the box to the minimum and maximum values, excluding outliers.
Skewness
- A box and whisker plot can reveal skewness in the data.
- If the median is closer to one end of the box, the data is skewed towards the opposite end.
Outliers
- Outliers are extreme values that lie outside the whiskers.
- They can indicate data errors or unique characteristics in the dataset.
By interpreting these elements, a box and whisker plot provides a comprehensive overview of the data distribution, enabling researchers to make informed inferences about the underlying population.
Creating a Box and Whisker Plot
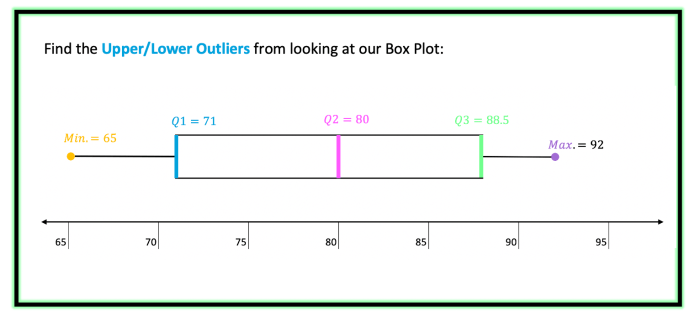
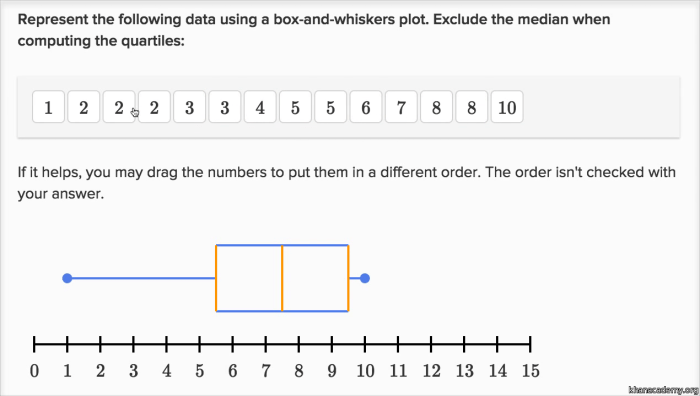
Creating a box and whisker plot involves organizing the data, calculating quartiles, and drawing the plot. Here’s a step-by-step procedure:
Organizing Data
Arrange the data in ascending order, from smallest to largest. If there are any duplicate values, treat them as separate data points.
Calculating Quartiles
- First quartile (Q1):The median of the lower half of the data.
- Second quartile (Q2):The median of the entire data set (also known as the median).
- Third quartile (Q3):The median of the upper half of the data.
The interquartile range (IQR) is the difference between Q3 and Q1, representing the spread of the middle 50% of the data.
Drawing the Plot
- Draw a horizontal line representing the median (Q2).
- Draw a box from Q1 to Q3.
- Draw a vertical line from the lower quartile (Q1) to the smallest data point that is within 1.5 times the IQR below Q1.
- Draw a vertical line from the upper quartile (Q3) to the largest data point that is within 1.5 times the IQR above Q3.
- Any data points outside these lines are considered outliers and are plotted individually as dots.
Applications of Box and Whisker Plots

Box and whisker plots are versatile graphical tools with wide applications across various fields, including statistics, data analysis, and quality control.
These plots are particularly useful for comparing multiple datasets, identifying trends, and making informed decisions based on data distribution and variability.
Data Comparison
- Box and whisker plots allow for easy visual comparison of multiple datasets, highlighting similarities and differences in their distributions.
- By comparing the medians, interquartile ranges, and outliers, researchers can quickly identify patterns and trends in the data.
Trend Identification, Box and whisker plot quiz
- Over time, box and whisker plots can be used to track changes in data distribution and identify trends.
- By comparing plots from different time points, analysts can monitor shifts in the median, spread, and presence of outliers.
Decision Making
- In quality control, box and whisker plots help identify outliers and potential defects in manufacturing processes.
- By analyzing the distribution of measurements, engineers can determine if the process is stable and meets quality standards.
FAQ Corner
What is the purpose of a box and whisker plot?
To provide a visual representation of the distribution of data, including its central tendency, spread, and the presence of outliers.
How do I identify the median in a box and whisker plot?
The median is represented by the line that divides the box into two equal halves.
What do the whiskers in a box and whisker plot indicate?
The whiskers extend from the quartiles to the minimum and maximum values, showing the range of the data.